An animated description of Landau damping

When an electron plasma wave passes through a plasma with a high enough temperature at a low enough phase velocity, its energy is siphoned into the plasma, and the wave decays. This is Landau damping, one of the most infamous plasma physics phenomena known to science. While the concept is relatively simple, explaining the mechanism in words invariably leads to oversimplification, and explaining it in math is surprisingly involved. That said, a reasonably accurate description of nonlinear Landau damping can be obtained by observing the trapping of electrons in phase space.

Start with a uniform one-dimensional plasma in thermal equilibrium. The electrons have normally-distributed velocities, and each moves eternally in a straight line with the velocity it was born with. We can plot the electron distribution in phase-space.

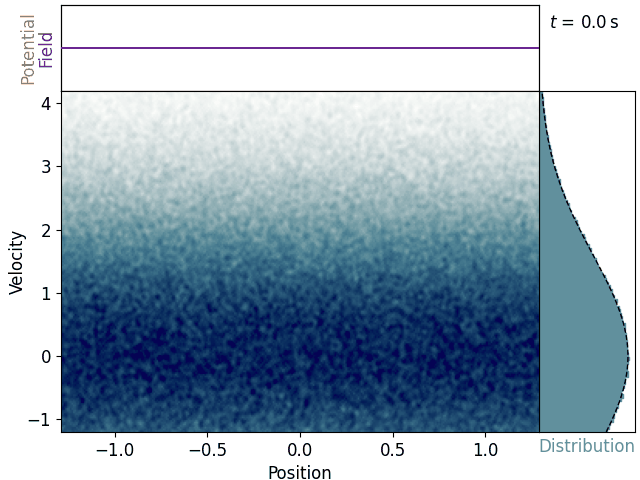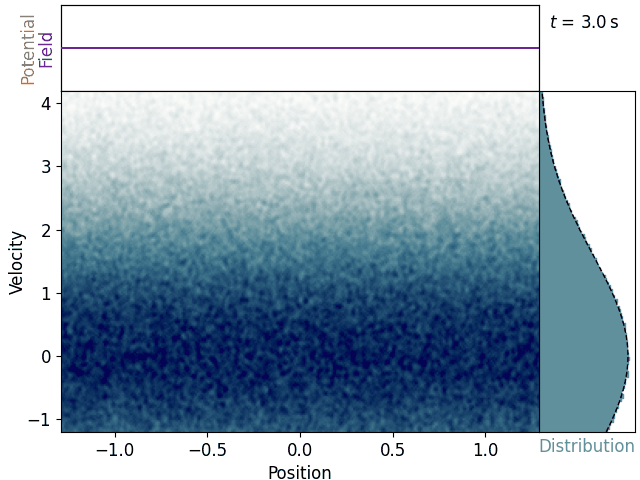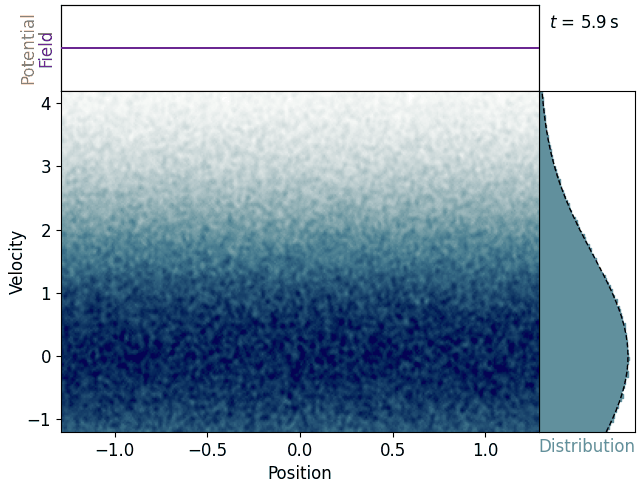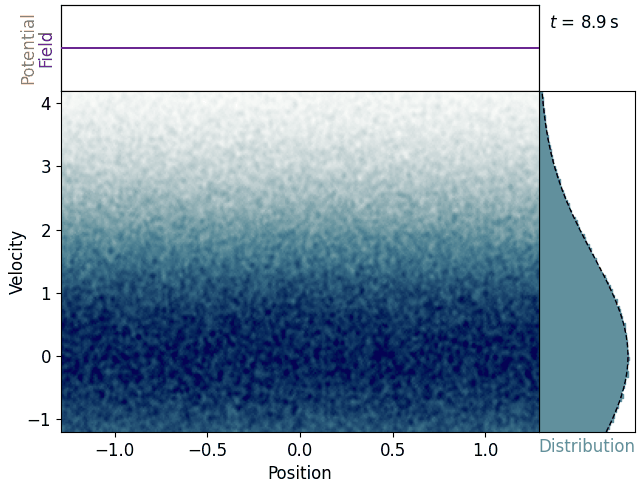
Let’s suppose that at some time, a longitudinal electrostatic plane wave is suddenly imposed. We’ll give it a constant wave number of k, frequency of 2πω, and amplitude of E₀. Each electron now feels an acceleration depending on where in the wave’s phase it happens to be at any given time. Let’s assume the ions are stationary, and let’s ignore the forces of the electrons on each other – both collisions and collective effects – such that each electron’s trajectory is a simple initial-value problem.

This is obviously not a realistic set-up. For one thing, electrostatic waves in this regime are plasma oscillations, which don’t just suddenly appear in a uniform plasma – they arise from the motion of the electrons. More importantly, asserting that the amplitude is constant seems to defeat the point of the exercise, which is to see the wave decay.

This arrangement is not entirely unphysical, though. We can suppose an external force is keeping the wave in place, allowing us to only worry about the electrons’ response. If the electrons gain energy, we can surmise that the external force is expending energy, and thus infer that a more realistic wave would be damped. We miss out on transient effects this way, but the acceleration of individual electrons in the wave is the main effect of interest, and accounting for other effects only complicates the picture without substantially changing the result.

With that said, let’s go back to our phase-space plot and see how the electrons react when the wave is turned on.

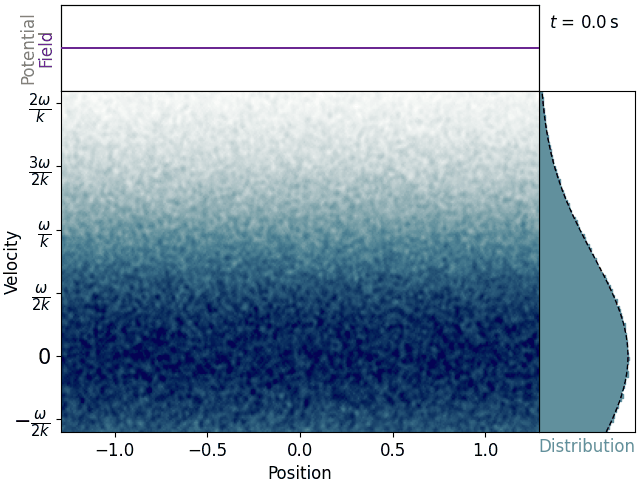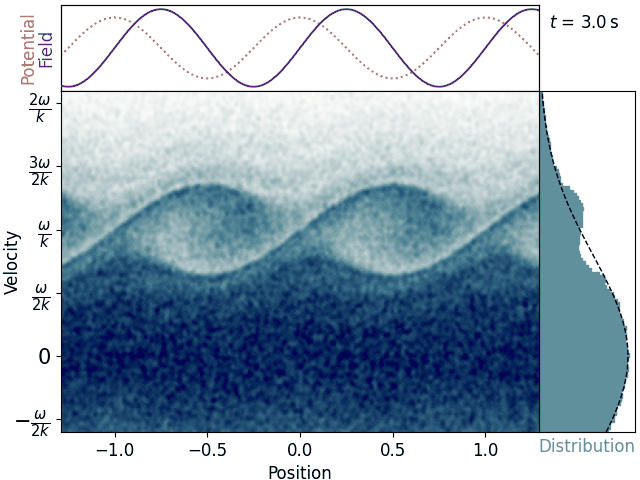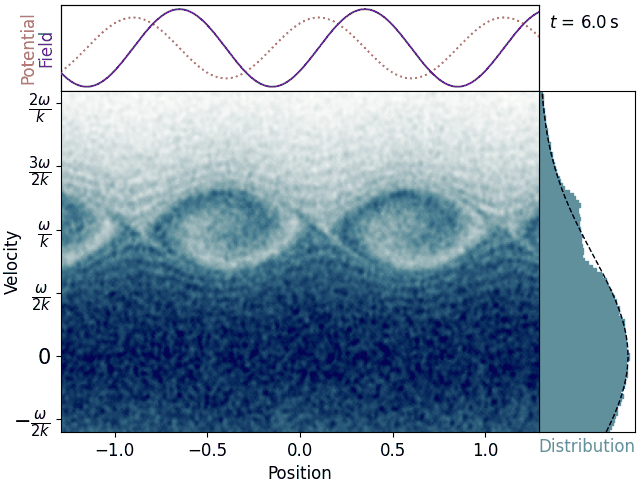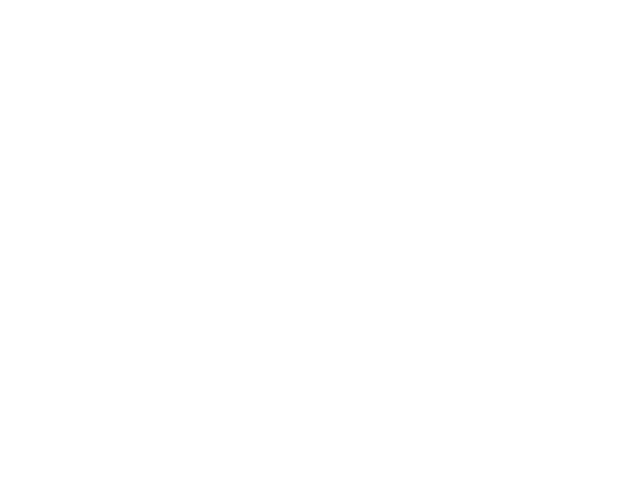
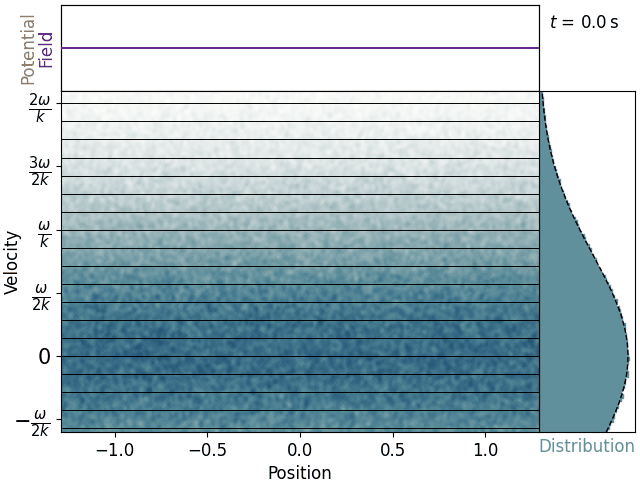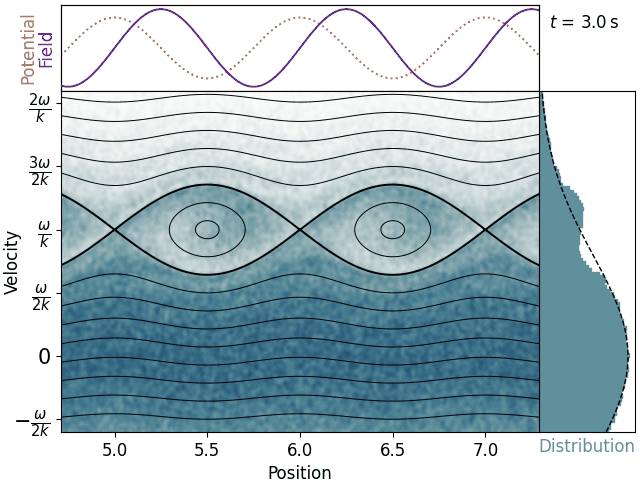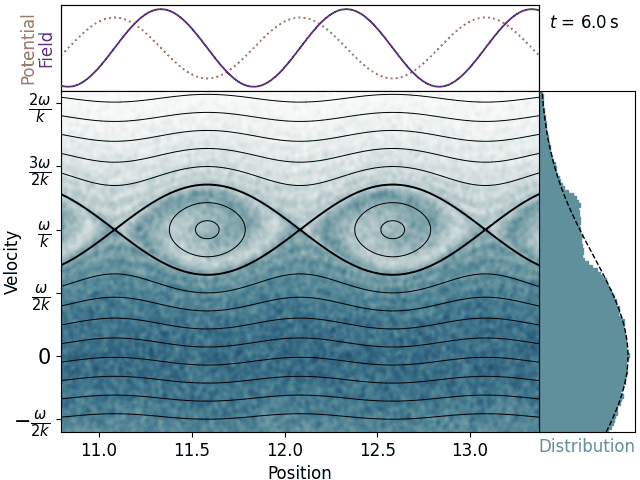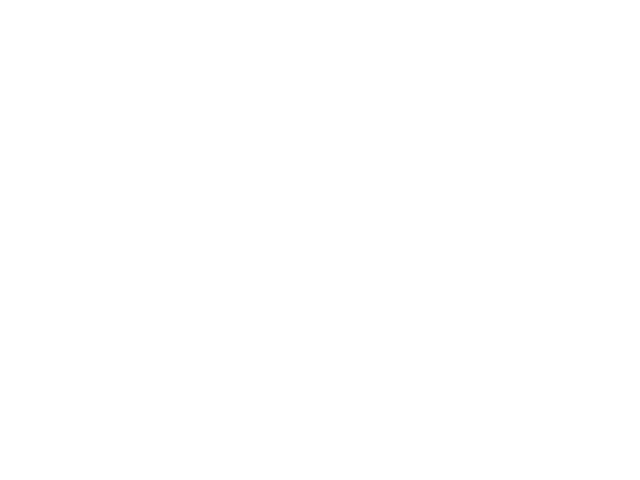
Most electrons wobble up and down as their velocities are perturbed by the alternating electric field. These stay near the velocity they were born with and thus don’t really interact with the wave. Near the wave’s phase velocity, though, we see some clumps of electrons reaching up like fingers and swirling around. This also becomes apparent in the velocity histogram, where a distinct plateau arises – the distribution is depleted just below the phase velocity and augmented just above it.

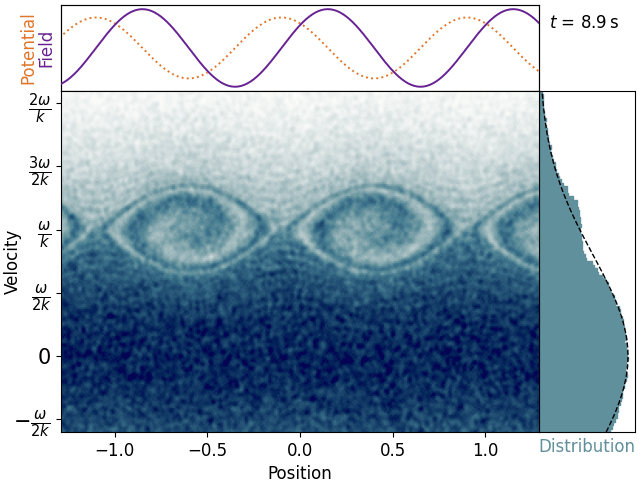
This is promising, since if clumps of electrons are moving up in velocity, they must be gaining energy, so the wave must be losing energy, just as according to keikaku. Vwallah, Landau damping! Seeing the simulation exhibit this effect doesn’t really help us understand why it’s happening, though.

So let’s dig deeper. We can get a better look at those finger things if we move our head with the wave. Here’s the same plot in the wave’s frame of reference.

In this frame, the wavefronts are stationary, and can be visualized as a fixed potential profile composed of many hills and wells. Since we’re in phase space, we can make a streamline plot of the electron trajectories.

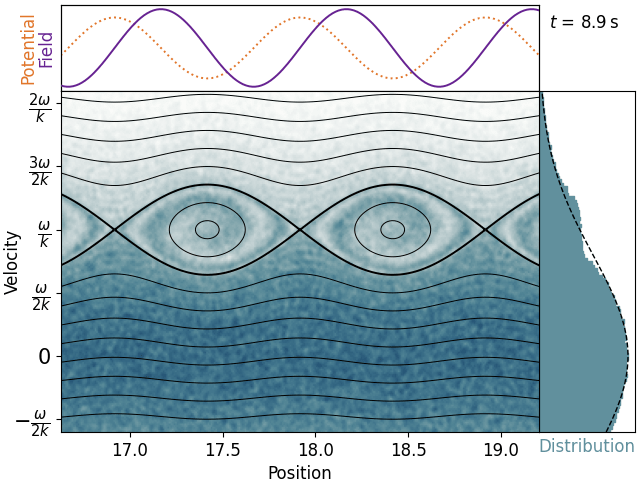
When we put it like this, two types of trajectories become apparent. Electrons above or below the thick eye-shaped wells are passing. They have enough kinetic energy relative to the wavefronts that they can get over each hill and move onto the next one. They might be sped up or slowed down a little bit, but overall they continue on with approximately the same velocity they were born with.

Electrons inside the thick eye-shaped wells, on the other hand, are trapped. These have too little kinetic energy in the wave frame, and are too close to the bottom of the potential well when it appears, such that they cannot reach the top of a hill. Instead, these electrons are doomed to bounce back and forth within a single well for all eternity. Critically, since they cannot make any forward or backwards progress in the wave frame, they must have an average velocity of zero. Or to put it in the lab frame, becuase they’re forced to move with the wavefronts, they must have an average velocity equal to the phase velocity. This means that trapped electrons that started below the phase velocity have been accelerated, and trapped electrons that started above the phase velocity have been decelerated. Since we started with more slow electrons than fast electrons, this means that the plasma gains energy and the wave is damped.

Of course, that’s all only if you average over a large number of bounces. You can actually see the trapped electrons oscillate up and down, strengthening and weakening the plateau with time. This causes an oscillation of the damping rate in time – a lesser-known but real feature of nonlinear Landau damping.

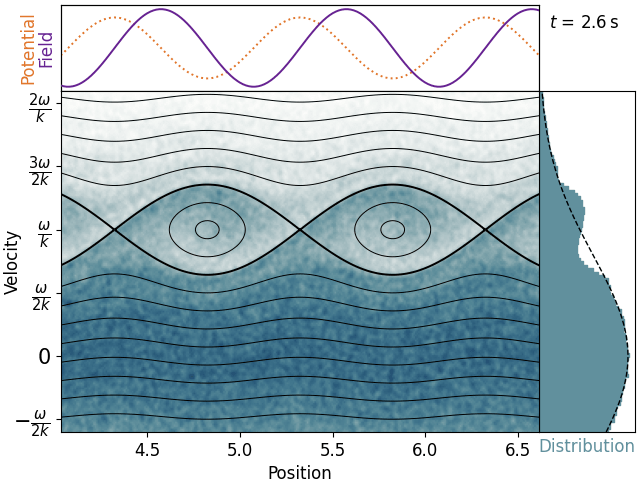
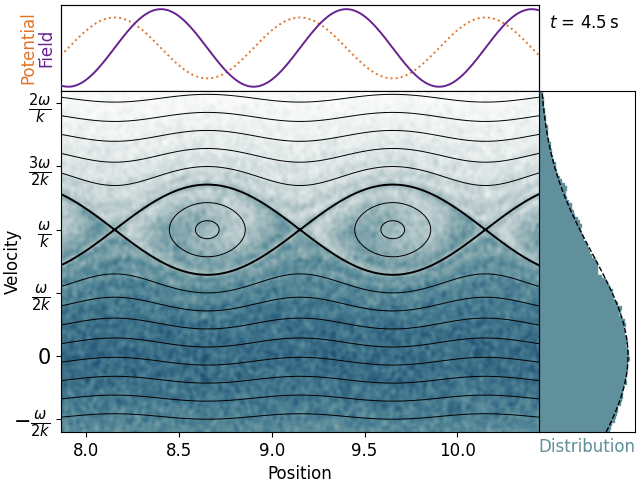
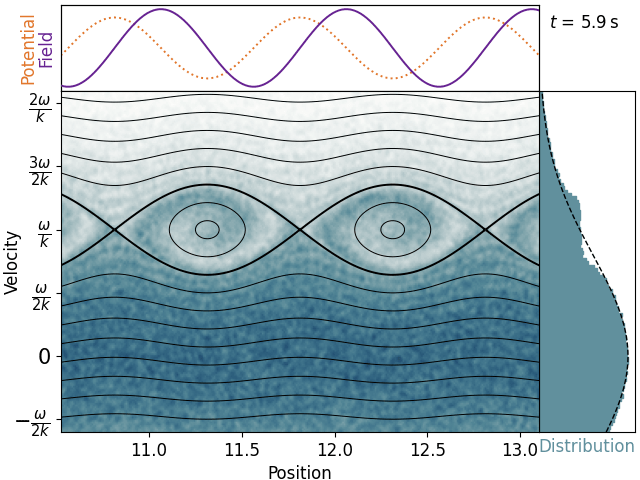
Another important transient effect we can see here is that the damping eventually saturates. If the wave is strong enough and we wait long enough, the trapped electrons will be thoroughly smeared across their well in phase space, and there will be no further gain or loss of energy. This can be counteracted by collisions, which will pull trapped electrons back into the thermal distribution and allow the damping to continue.

Even within this simplified representation, electron trapping is still only part of the picture. If you look closely, you might note that even passing electrons, both above and below the phase velocity, gain energy on average. This is a consequence of the fact that electrons are both accelerated and decelerated by the wave. Electrons of all energies are somewhat mixed together in velocity space. It can be shown without much math that as long as there are initially more slow electrons than fast electrons, this mixing will always lead to an acceleration on average. This result is important because it helps to explain linear Landau damping, which occurs when the wave amplitude is too small to trap electrons. That’s out of the scope of this article, though, since it doesn’t come through very clearly in these animated plots.

While the picture presented here is highly simplified, it captures the main physics responsible for nonlinear Landau damping. Hopefully it’s given you with a more intuitive understanding of how and why it arises, such that you can better respond the next time a plasma wave comes at you in the wild. Or at the very least, I hope you found the plots pretty.

Edit: Tim said I shouldn’t talk about the wave’s “velocity” without specifying which velocity.